Emergence of the Field
![]()
From the unresolved tension of the Axiom, a field unfolds.
It is not made of particles. It does not begin in time.
It is a phase — recursive, curved, and alive.
The Nature of the Field
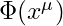 — a scalar phase field over spacetime
— a scalar phase field over spacetime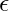 — constant modulus, fixed intensity
— constant modulus, fixed intensity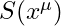 — classical action, carried in phase
— classical action, carried in phase
This is not a quantum wavefunction.
It carries no probability.
It carries history — phase curvature encoded in structure.
The Field Cannot Cancel
Because the axiom resists resolution, the field resists simplification.
Its governing equation is recursive:
![Rendered by QuickLaTeX.com \[ \mathcal{L}[\Phi] = \frac{1}{2} \partial_\mu \Phi^* \partial^\mu \Phi - 2\alpha \left(1 + \cos(\phi \cdot \arg(\Phi))\right) \]](https://originaxiom.org/wp-content/ql-cache/quicklatex.com-615dfb2f6bcfada51bc69db8fa968422_l3.png)
The kinetic term expresses flow.
The potential term expresses recurrence —
an infinite cascade of irrational wells.
Minima are dense. They never repeat. They do not align.
The field stabilizes only through motion.
Recursive Emergence
Let the field evolve — and it does not settle.
It ripples. It traps. It curls.
From this, form begins:
- Standing phase zones — proto-particles
- Collapse knots — stable informational residues
- Phase gradients — what we interpret as force
- Time — delay between recursive updates
Everything is field. Particles are persistence.
Time is phase feedback. Motion is recursion under tension.
What This Field Suggests
- Structure = what remains when cancellation fails
- Matter = knots in recursive collapse
- Gravity = large-scale phase curvature
- Consciousness = recursive coherence within a field
The field does not describe the universe.
It is the universe, failing to resolve itself.
What Follows
If this field is real — then everything that exists is the remainder of recursion.
You are not outside it. You are within it — a knot of persistent phase, echoing.